Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.

Network and Graph Theory - Critical path.
Test Yourself 1.


 

Given a diagram. 1. Answer.9 edges.
  2. Answer.14 edges.
  3. Answer.11 vertices.
Determining float time. 4.
   
  6.
   
  2019 HSC Sample
   
  10. Answer.Vertex D has degree 4.
Determining the Critical path 11.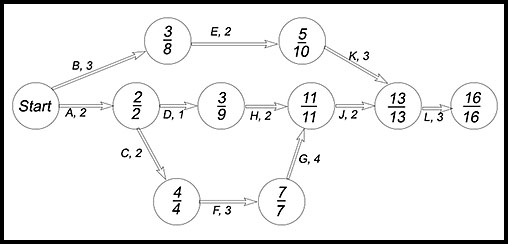

The sequence required to implement a building project is summarised in the diagram above.

The activities to be completed are named along each edge together with the time required to complete that activity. The earliest start and latest finish times are summarised in the nodes.

With reference to the information provided in the diagram:

(i) How many weeks is the entire building project expect to take?

(ii) What is the earliest start time for task H?

(iii) What series of tasks forms the critical path?

(iv) What is the float time for task E?

(v) Early in the project, a delay occurs which means that Task D cannot be started until week 5. Explain the impact that this delay will have on the expected completion time of the project.

Answer.(i) 16 weeks.
(ii) Week 3.
(iii) The CP is A-C-F-G-J-L.
(iv) 5 weeks.
(v) No imact because the float time for Activity D is 6 weeks which is less than the delay in starting. In addition, Activity D is not on the critical path.
  12.

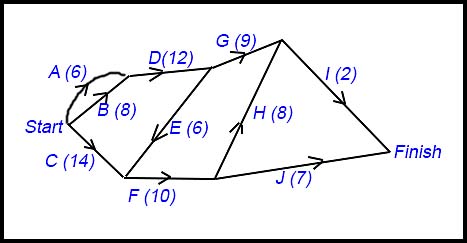
The above diagram shows the network of 10 activities required to complete a particular task. The time in days to complete each activity is shown in brackets.

(i) What is the minimum time needed to complete the task?

(ii) Which activities make up the critical path for this task?

(iii) What is the Earliest Start Time and the Float Time for:

  • Activity C;
  • Activity F.
Answer.(i) 46 weeks.
(ii) Critical path is A, D, E, F, H, I.
(iii) For C: Earliest start is
0 weeks and Float Time is
26 - 14 = 12 weeks
For F: Earliest start time is
26 weeks and Float time
is 0 weeks (on CP).
   
   
   
Determining slack, etc